We are extending to 3D (algebraic surfaces) the 3L fitting algorithm originally designed for 2D shapes (algebraic curves). A 3D implicit polynomial surface is fit to a data set which can represent a closed surface or an open 3D surface patch. The fitting is linear, approximately least-squares with the result that the computation is modest and non-iterative. With the algorithm, the polynomial coefficients are much more stable and repeatable, than are the results with other current fitting methods, under small changes in the data sets to be fit. Fitting is done using polynomials with degrees ranging from 1 to 12 so that either very crude or fairly high resolution shape information can be captured with a single polynomial.


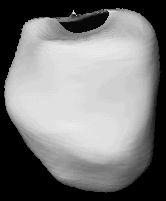
Original heart and 8th degree fit.


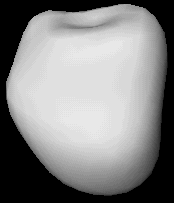
Original head and 10th degree fit.
Using this model, to compute the shape alignment an intrinsic coordinate system is formed by computing a center and a set of three coordinate axes for the implicit surface. This computation is based on multi-algebra properties of the algebraic surface in its tensorial representation. This is a one shot computation, and the resulting coordinate system can then be aligned by a single computation with an analogously computed intrinsic coordinate system for another 3D shape. The two aligned 3D representations or data sets can then be compared very accurately at low computational cost.
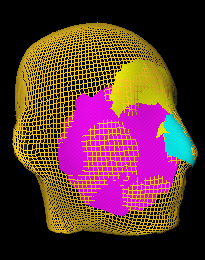




Head data; IP fits to Maximum Radius Invariant Patches for nose, cheek, eye and nose test location.
The test patch (in red) is aligned with each of the other patches through the single-computation alignment proceedure, then it is fine aligned with a few iterations of gradient descent using the PIMs performance measure, and then the test patch is PIMs compared with each of the three stored patches with which it has been aligned. The distance to the overlapping nose patch is an order of magnitude less than the distances to the other two patches. This alignment and matching proceedure is very fast and highly accurate.
Last updated: June 3, 1998
Back to research topics.