Calibration data:

Assuming a pin-hole camera model, the transformation between 3D space and image is a perspective projection.

Description:

The set of the calibration parameters is: u0, v0, au, av, R and T (see figure 1).

Internal or intrinsic parameters are:

• (u0,v0): coordinates in pixels of the image center which is the projection of the camera center on the retina.
• (au,av): scale factors of the image. The vertical and horizontal steps of digitization are 1/av and 1/au respectively, in mm.
• (dimx, dimy) : size in pixel of the image.

All parameters are theoritically expressed in focal length unit. For reasons of simplicity the focal length is here assumed to be 1mm.

External or extrinsic parameters are:

• R: rotation which gives axes of the camera in the reference coordinate system.
• T: pose in mm of the camera center in the reference coordinate system.

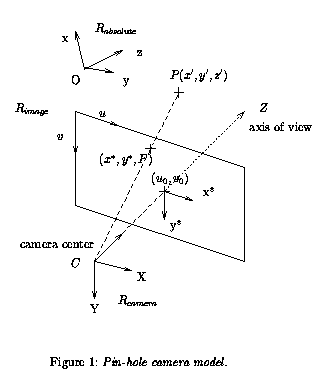
How compute the projection matrix?

For each 3D point X in the reference coordinate frame, its image (u,v) in pixel is:

u = u0 + au x'/z'
v = v0 + av y'/z'

where X' = (x',y',z') are the coordinates of the 3D point in the camera coordinate system. Thus, they are linked with X by the following equation R X' + T = X.

Consequently, with our notations, the perspective transformation matrix between 3D and 2D homogeneous coordinates is:

{u s, v s, s} = {{au, 0, u0, 0}, {0, av, v0, 0}, {0, 0, 1, 0}} inverse({{R, T}, {0, 1}}) {X, 1}

A technical manual of the calibration software is available.